← advait.org

Abstract

Spreadsheet errors are ubiquitous and costly, an unfortunate combination that is well-reported. A large class of these errors can be attributed to the inability to clearly see the underlying computational structure, as well as poor support for abstraction (encapsulation, re-use, etc). In this paper we propose a novel solution: a multiple-representation spreadsheet containing additional representations that allow abstract operations, without altering the conventional grid representation or its formula syntax. Through a user study, we demonstrate that the use of multiple representations can significantly improve user performance when performing spreadsheet authoring and debugging tasks. We close with a discussion of design implications and outline future directions for this line of inquiry.

1 Introduction

Spreadsheets excel at showing data, while hiding computation. In many ways the emphasis on showing data is a huge advantage, but it comes with serious difficulties: because the computations are hidden, spreadsheets are hard to understand, explain, debug, audit, and maintain.

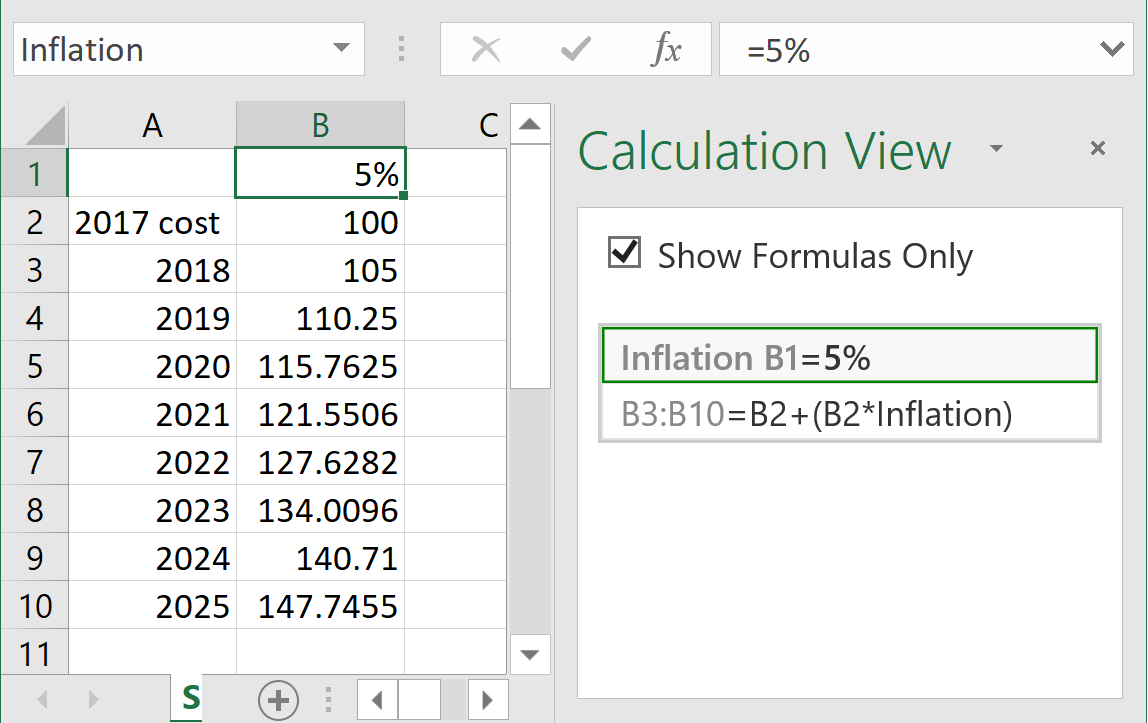
It is often remarked that “spreadsheets are code” [1]. What would happen if we take that idea seriously, and offer a view of the spreadsheet designed primarily to display its computational structure? Then, in this Calculation View, we might be able to offer more abstract operations on ranges within the grid, and alternative ways to achieve useful tasks that are cumbersome or error-prone in the grid view. We have designed, prototyped, and evaluated just such a feature (Fig. 1). More specifically, we make the following contributions.

• We present a design for a view of a spreadsheet primarily intended for viewing formulas and their groupings. Edits to either the grid or to Calculation View show up immediately in the other. This design and its possible variants are discussed in the context of the theory of multiple representations (Sections 3 and 4).

• We describe two particularly compelling advantages of Calculation View:

  • Calculation View improves on error-prone copy/paste (Section 3.2) using range assignment: a new textual syntax for copying a formula into a block of cells.

  • Calculation View offers a simple syntax for naming cells or ranges, and referring to those names in other formulas (Section 3.3). Naming is available in spreadsheets such as Excel, but few users exploit it because of the high interaction cost.

• We present the results of a user study (Section 5) showing that certain common classes of spreadsheet authoring and debugging tasks are faster when users have access to Calculation View, with lower cognitive load, without reduction in self-efficacy.

We regard Calculation View as a first step in a rich space of multiple-representation designs that can enable new experiences in spreadsheets, discussed further in Section 6.

2 The problem and our approach

2.1 Problem: errors in spreadsheets

As with any large body of code, spreadsheets contain errors of many kinds, with often catastrophic implications, given the heavy dependence on spreadsheets in many domains. The ubiquity and maleficence of spreadsheet errors has been well documented [2], and there are even specialised conferences dedicated solely to spreadsheet errors!¹

We focus on the following specific difficulties, using the vocabulary of cognitive dimensions [3]:

1. Invisibility of computational structure. The graphical display of the sheet does not intrinsically convey how values are computed, which groups of cells have shared formulas, and how cells depend on each other. This creates hidden dependencies in the sheet’s dataflow. Apart from individually inspecting cell formulas, or relying on secondary notation provided by the spreadsheet author (layout, borders, whitespace, colouring, etc.), there are no affordances for auditing the calculations of a spreadsheet, which makes auditing tedious and error-prone. Visibility suffers in large spreadsheets; the display is typically too small to contain all formulas at once. Visibility is also impaired by the inability to display formulas and their results simultaneously; the user must inspect formulas individually using the formula bar. The “Show formulas” option, which displays each cell’s formula in the cell instead of the computed value, is also impractical, since the length of formulas typically exceeds the cell width, leading to truncation.

2. Poor support for abstraction. Consider the following common form of spreadsheet:

   Data	Formula 1	Formula 2	...	Formula k
   d1	F1(d1)	F2(d1)	...	Fk(d1)
   d2	F1(d2)	F2(d2)	...	Fk(d2)
   ...	...	...	...	...
   dn	F1(dn)	F2(dn)	...	Fk(dn)

   The first column is a list of data, and each other column simply computes something from the base data. The formulas in each row repeat the calculation for the data in that row; rows are independent. There are only as many distinct formulas as there are columns; the complexity of building and testing this spreadsheet should not be affected by whether there are ten rows, or ten million. The user experience, unfortunately, is deeply affected. The notation is error prone in that the user is responsible for manually ensuring that the column formula is precisely copied the correct number of rows. Any subsequent edits to column formulas are viscous as well as error prone, as they must be correctly propagated to the correct range, which involves identifying all the cells that the author intended to contain that formula, an intention for which there is usually no explicit record.

3. Formulas suffer from a lack of readable names. Grid cell references (e.g., A1, B2, etc.) are terrible variable names, as they contain no information regarding what the value in the cell might represent. They can be easily mistyped as other valid grid cell references, leading to a silent error. Conventional programming languages allow users to give domain-relevant names to their values (improving closeness-of-mapping); for example, we might want to refer to cell B2 as TaxRate – a simple form of abstraction. Some spreadsheet packages do in fact support naming cells and cell ranges (e.g., Excel’s name manager²) but these features are not widely used due to high additional interaction and cognitive costs: of naming cells; of recalling what cells have been named; and remembering to actually use the name (i.e., not mixing usage of the name and the cell it refers to).

2.2 Our approach: augmenting the grid

Previous approaches to mitigating errors in spreadsheets have focused either on auditing tools, or on modifying the grid and its formula syntax (see Section 7). In this paper, we present an exploration of a fundamentally new approach to the problem. We propose that the grid, and its formula syntax, be left untouched, but to provide opportunities for abstraction through additional representations. We build on the theory of multiple representations that originates in Ainsworth’s research in mathematics education [4] but has found widespread applications in computer science education [5], [6], and end-user programming research [7]. By offering multiple representations of the same core object (in our case, the program exemplified by the spreadsheet), we can help the user learn to move fluently between different levels of abstraction, choosing the abstraction appropriate for the task at hand.

3 Textual notation in Calculation View

Thus motivated, we created an alternative representation, Calculation View, or CV for short, of the spreadsheet as a textual program. CV is displayed in a pane adjacent to the grid. In CV, the grid is described as a set of formula assignments. For example:

    B1 = SQRT(A1)

assigns the formula =SQRT(A1) to the cell B1. Edits in one view are immediately propagated to the other and the spreadsheet is recalculated; it is live [8].

3.1 Review: formula copy-and-paste in spreadsheets

Before we introduce a new, more powerful type of assignment in CV, it is helpful to review the distinctive behaviour of copy-and-paste in spreadsheets today.

Suppose that cells A1 to A10 contain some numbers, and the user wishes to compute the square root of each of these numbers in column B. The user would begin by typing =SQRT(A1) into cell B1. They could type =SQRT(A2) into cell B2, and so on, but a more efficient method is to copy =SQRT(A1) from cell B1 and paste into B2. The user intention is not to paste the same literal formula, but rather one that is updated to point to the corresponding cell in A. The operation of formula copy-and-paste rewrites the formula =SQRT(A1) into the intended form =SQRT(A2).

This is achieved by interpreting references in the original formula as spatially relative to the cell, as can be expressed using “R1C1” notation. For example, the expression SQRT(A1) occurring in cell B1 is represented as SQRT(R[0]C[-1]) in R1C1, because with respect to B1, A1 represents the cell in the same row (R[0]) and the previous column (C[-1]). This formula pasted into the cells B2 to B10 becomes the sequence SQRT(A2), …, SQRT(A10); the relative reference resolves into a different cell reference for each case. Spreadsheet packages generally allow this behaviour to be overridden (e.g., Excel’s absolute references³).

The drag-fill operation builds on formula copy-and-paste. In a drag-fill, the user types =SQRT(A1) into cell B1, selects it, and then drags down to cover the range B1:B10, which is equivalent to copying B1 into each cell in the range.

Copy/paste and drag-fill enable the user to create computations on arrays and matrices without needing to understand functional programming formalisms such as map, fold, and scan. However, the conceptual abstraction of arrays is not reflected in any grid affordances; it is easy to accidentally omit cells or overextend the drag-filling operation, and the user must manually propagate any changes in the formula to all participating cells – a fiddly and error-prone process.

CV, being separate from the grid, presents an opportunity to allow abstract operations on arrays and matrices without affecting the usability of the grid.

3.2 First idea: range assignments

The first novel affordance of our notation is range assignment, which assigns the same formula to a range of cells just as a drag-fill copies a single formula to a range. In CV, the user could accomplish the previous example using the following range assignment:

    B1:B10 = SQRT(A1)

The colon symbol is already used in Excel to denote a range, and so its use capitalises on users’ existing syntax vocabulary.

The assignment has an effect identical to entering the formula =SQRT(A1) into the top-left cell of the range B1:B10, and then drag-filling over the rest of the range. Observe how our syntax uses the literal formula for the top-left cell; users must apply their mental model of formula copy-and-paste to predict how the formula will behave for the rest of the range. In this manner, range assignment exposes a low-abstraction syntax for array/matrix assignment.

An alternative, that does not rely on knowledge of copy-paste semantics, would be to use R1C1 notation:

    B1:B10 = SQRT(R[0]C[-1])

This is clearer, because the same formula is assigned to every cell, but understanding the formula requires knowledge of the more abstract R1C1 notation.

Range assignment has many benefits. It is less diffuse/verbose, as it represents all formulas in a block using a single formula. It has a greater closeness-of-mapping to user intent. It greatly improves visibility of the formulas in the sheet (take for example our sheet with one formula per column – even with thousands of rows, the CV representation shows a single range assignment per column). Moreover, the representation greatly reduces the viscosity and error-proneness of editing a block of formulas. Instead of manual copying or drag-filling, the user simply edits the formula in the range assignment. The range itself can also be edited to adjust the extent of the copied formula precisely and easily.

3.3 Second idea: cell naming

The lack of meaningful names for grid cell references leads to unreadability and error proneness in formulas. Extant naming features in spreadsheet packages are seldom used in practice; CV presents an opportunity to drastically lower the interactional and cognitive costs for using names. To name a cell or range, the user employs the following syntax:

    Name Cell = Formula

A concrete example is this:

    TaxRate A1 = 0.01

which puts the value 0.01 into cell A1 and gives it the name TaxRate. Thus to compute tax, one can write the formula in terms of TaxRate rather than A1, which is more readable, more memorable, more intelligible, and more difficult to mistype as a different but valid reference. We considered alternative naming syntaxes (e.g., TaxRate[A1] = ...; TaxRate in A1 = ...; A1 as TaxRate = ...; TaxRate = A1 = ...; etc.) and a detailed investigation of this would make for interesting future work, but within the scope of our initial exploration we settled on the simple space-delimited syntax for its readability.

3.4 Summary syntax and semantics for Calculation View

Cell ::= $A1$-$notation$
            Range ::= Cell | Cell:Cell

Literal ::= $number$ | $string$
            Name ::= $identifier$
            Fun ::= SUM | SQRT | ...
            Formula ::=
                Literal | Range | Name | Fun(Formula$_1$, ..., Formula$_N$) | ...

Assignment ::=
                Range = Formula |
                Name Range = Formula
            Program ::= Assignment$_1$ ... Assignment$_N$

Figure 2 shows the complete grammar of the textual notation in our initial implementation of Calculation View.

Our language has a simple semantics, as follows. An assignment Range = Formula is equivalent to entering =Formula into the top-left cell of Range, and pasting that formula to every other cell in Range. An assignment Name Range = Formula additionally binds the name Name to the range Range.

We require that no two assignments target the same cell. We place other constraints on the program including that each range targets a non-empty set of cells.

4 Interaction design in Calculation View

4.1 Use of multiple representations

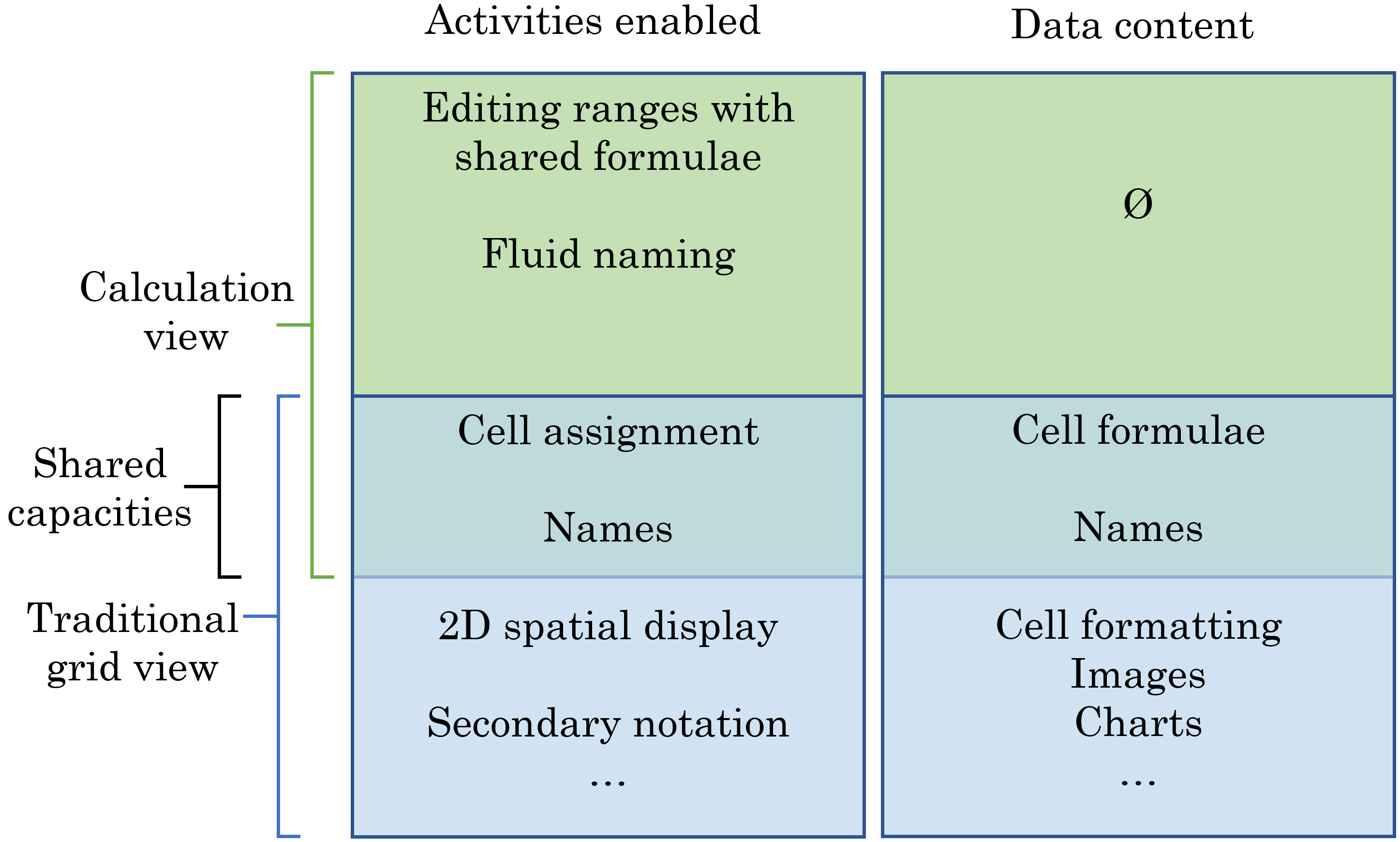
“Multiple representations” is a broad umbrella term for systems that show some shared concept in multiple ways, but this can have a variety of different manifestations, depending on how tightly coupled the representations are, what underlying concepts they share, and other design variables. CV’s specific use of multiple representations – in particular, what functions CV does, and does not perform – can be characterised in terms of Ainsworth’s functional taxonomy for multiple-representation environments [4]:

• Complementary roles through complementary tasks. In CV, these tasks are: creating and editing formulas, creating and editing ranges of shared formulas, and viewing the computational structure of the sheet. In the grid view, these tasks are: setting cell formatting, layout, and other secondary notation to prepare the data for display, inserting charts and other non-formula entities, etc. CV and the grid facilitate complementary strategies; the primary strategy for range editing in the grid is copy/paste or drag-fill, which is well suited for small ranges and for visual display of data. In CV, the primary strategy is to use range assignment, which is well suited for robust editing of ranges with shared formulas.

• Complementary information: CV can display formulas while the grid displays data and formula output.

• CV constructs deeper understanding using abstraction through reification: a type of abstraction where a process at one level is reconceived as an object at a higher level [9]. In spreadsheets, users understand a range of shared formulas as a single abstract entity; the process of copy/paste or drag-filling at the cell level creates an object at the range level. In CV, we build on that understanding and reify those ranges as single objects.

Our model of shared representation is depicted in Figure 3. Both CV and the grid share certain features, such as the ability to assign names, and the ability to assign formulas to individual cells. However, CV allows range assignment and a naming syntax not possible in the standard grid. Similarly, CV does not have facilities for adjusting cell formatting, or viewing the spatial grid layout of formulas.

CV introduces no new information content to the spreadsheet; indeed, the CV is generated each time the spreadsheet is opened, or when the grid view is edited (see Section 4.3).

4.2 Editing experience design

CV departs from traditional text editors in a few deliberate ways. The first is the explicit visual distinction between lines, creating a columnar grid of pseudocells. This makes CV appear familiar, due to its similarity to the grid, and reinforces the fact that there should only be one assignment per line. Unlike many other programming languages, which permit multiple statements on a single line (delimited by, e.g., semicolons), Excel has no counterpart to this and so CV’s pseudocells help indicate the absence of that facility.

The second departure of CV from a simple text editor is the newline behaviour. In the Excel grid, hitting the enter (or return) key has the effect of committing the current formula and moving focus to the next cell down. If this same behaviour were adopted wholesale into CV, then hitting enter would only navigate between pseudocells, and additional interface components would be required to allow users to create new cell/range assignments. Instead, in our design, hitting enter while any pseudocell is in focus creates a new pseudocell underneath it, combining the properties of a flat text editor and the grid. Pseudocells can only be empty while they are being edited. If a pseudocell is empty when it loses focus, it disappears. Thus, cell and range assignments can be deleted by deleting the contents of the corresponding pseudocell, and when the pseudocell loses focus, it disappears from CV and so do its formulas on the grid. Another aspect of this design is that unlike in a text editor, where multiple blank lines can be entered by repeatedly hitting enter, in CV repeatedly hitting enter does nothing after the initial empty pseudocell is created – no new pseudocells will be created while an empty pseudocell is in focus.

We acknowledge, however, that the free addition of whitespace and re-ordering of statements is a valuable form of secondary notation in textual programming languages. In future work it would be useful to compare a version of CV presented as a simple text editor, with the pseudocell representation we have created (Section 6).

4.3 Block detection algorithm

It is not sufficient for CV to only display range assignments created in the CV editor. In order to fully capitalise on the increased abstraction possible in CV, any block of copied/drag-filled formulas, even if these operations were performed manually in grid view, should also be represented in CV as a range assignment. We implemented a simple block detection algorithm to achieve this. The algorithm operates as follows: the cells in the sheet are first placed into R1C1 equivalence classes (i.e., cells with the same formula in R1C1 are grouped into the same class. Then, for each class, maximal rectangular ranges (called ‘blocks’) are detected using a greedy flood-filling operation: the top-left cell in the class is chosen to ‘seed’ the block. The cell to the right of the seed is checked; if it belongs to the same class, then the block is grown to include it. This is repeated until the block has achieved a maximal left-right extent. The block is now grown vertically by checking if the corresponding cells in the row below are also part of the equivalence class. Once it can no longer be grown vertically, this maximal block is then ‘removed’ from the equivalence class. A new top-left seed is picked and grown, and the process is repeated until all the cells in the equivalence class have been assimilated as part of a block.

Each block so detected becomes a range assignment in CV. There are edge cases in which the behaviour of our algorithm is somewhat arbitrary. For instance, in an L-shaped region of cells containing R1C1-equivalent formulas, the ‘corner’ of this region could reasonably belong to either ‘arm’, but our greedy approach gives preference to the top-leftmost arm. Blocks of this shape are unusual in practice, and for our initial exploration, our basic approach has proven adequate.

4.4 Formula ordering

In what order should formulas be listed in CV? There are at least two straightforward options: (1) ordering by cell position (e.g., left to right, top to bottom) and (2) ordering by a topological sort of the formula dependency graph. Both options are viable: the former juxtaposes cells that are spatially related to each other, the latter juxtaposes cells that are logically related. In our investigation we have not addressed this design choice. For simplicity we adopted spatial ordering, but it may be better to allow the user to choose, or to choose using a heuristic characterisation of the spreadsheet.

The user can enter a newline in any pseudocell in CV to create a new pseudocell below it. The formula in this pseudocell can pertain to any cell or range in the grid, and will remain in the position it was entered until another cell in the grid (not CV) is selected, which triggers a regeneration of CV, at which point the formula is moved to its position according to spatial ordering. This is illustrated in Figure4.

Alternative designs are possible. For instance, the interface might make an exception for formulas entered in CV, remember their position relative to other formulas, and try to preserve that position as well as possible in order to prevent the jarring user experience of having their formula moved around. The problem of preserving position is nontrivial, and would make for interesting future work.

4.5 View filtering

Even after block detection has collapsed blocks of formulas into single pseudocells, there is still potential for CV to become cluttered. For instance, in the example from Section 2, if all the cells containing base data in the first column were displayed in CV, hundreds of pseudocells displaying base data would obscure the range assignments for the other columns – which are the main items of interest. To improve this, CV filters out literal values by default (with the option to show them if necessary). In future work, one might imagine advanced sorting and filtering functionality, such as “show only formulas within a certain range”, or “show only formulas containing some subexpression”, or “show formulas which evaluate to a certain type, e.g., boolean”, or even simpler options such as “sort by formula length”.

The key observation with respect to view filtering in CV is that, as in other multiple representation systems, each individual representation is suitable/superior for certain specific things. Here, the grid is a superb place to display lots of literal values; CV need not compete with the grid for doing that. CV is good at showing formulas and their abstract grouping, so it should have affordances for doing that well.

5 User study

CV aims to present a higher level of abstraction in spreadsheets without affecting the fundamental usability of the grid. We are interested in whether access to such a representation helps users create and reason about spreadsheets with less manual and cognitive effort.

We refined our research interests into the following concrete hypotheses. Does the addition of CV to the grid affect:

1. the time taken to author spreadsheets;

2. the time taken to debug spreadsheets;

3. the user self-efficacy in spreadsheet manipulation; and

4. the cognitive load for spreadsheet usage?

We are also interested in whether any observed difference is affected by the participant’s level of spreadsheet expertise.

5.1 Participants

We recruited 22 participants, between 25 and 45 years of age, 14 female and 8 male, using convenience sampling. Participants spanned four different organisations and worked in a range of professions including office administration, real estate planning and surveying, interaction design research, and civil engineering. All 22 had prior experience with spreadsheets and 18 used spreadsheets in regular work.

5.2 Tasks

We used two types of tasks: authoring and debugging. For the authoring tasks, participants were given a partially completed spreadsheet and asked to complete it. For each authoring task, completion involved writing between 1-3 simple formulas, and copying those formulas to fill certain ranges. We created 2 pairs of authoring tasks, where tasks within a pair were designed to be of equal difficulty. For instance, one task was for participants to calculate several years of appreciated prices for a list of real estate properties whose current values were given. The matched counterpart for this task was for participants to calculate several years of depreciated values for a list of company assets whose current values were given. Both require writing a formula of similar complexity and filling it to a range of similar size.

In debugging tasks, participants were given a completed spreadsheet and informed that there may be any of two types of errors: a copy/paste or drag-fill error where a row or column had been accidentally omitted or included, and a cell where a formula had been inadvertently overwritten using a fixed constant. The task was to detect any errors of these two types. We created 2 pairs of debugging tasks with matched difficulty. These tasks resembled the completed sheets that the participants were to create in the authoring task, so that the participant already understood what the purpose of the sheet was. In each task there was exactly one drag-fill error and one overwriting error, but participants were not informed of this.

5.3 Protocol

Participants were briefed and signed a consent form. They then completed a questionnaire about their spreadsheet and programming expertise, based on a questionnaire used in a previous study of program comprehension [10], but refactored to include items specific to spreadsheets. They were then given a 10-minute tutorial covering formulas and drag-filling in the standard public release of Microsoft Excel, as well as the range assignment syntax in CV, and given the opportunity to clarify their understanding with the experimenter.

Participants then completed four tasks: two authoring and two debugging tasks. Half the participants used Excel without CV and the other half used Excel with CV. After these tasks, participants completed standard questionnaires for cognitive load (NASA TLX [11]) and computer self-efficacy [12]. Participants completed a further four tasks, these being the matched counterparts to the tasks in the first round, this time with CV if they were without CV for the first round, or vice versa. After these tasks, participants again completed cognitive load and self-efficacy questionnaires.

The order in which participants encountered our experimental conditions (with or without CV) was balanced, and we could make a within-subjects comparison. The order in which tasks of each type were presented was counterbalanced. Within each task-pair, each task of the pair was assigned alternately to the with-CV and the without-CV condition.

The experiment lasted 70 minutes on average and participants were compensated £20 for their time.

5.4 Results

Task times: Participants took less time to complete spreadsheet authoring tasks when using CV than without (median difference of -54 seconds, or a median speed-up of 37.14%). This difference is statistically significant (Wilcoxon signed rank test: Z =  − 4.14,p = 3.6 ⋅ 10⁻⁵ ). See Figure 5.

Participants took less time to complete spreadsheet debugging tasks when using CV than without (median difference of -20 seconds, or a median speed-up of 40.7%). This difference is statistically significant (Wilcoxon signed rank test: Z =  − 3.3,p = 9.6 ⋅ 10⁻⁴ ). See Figure 5.

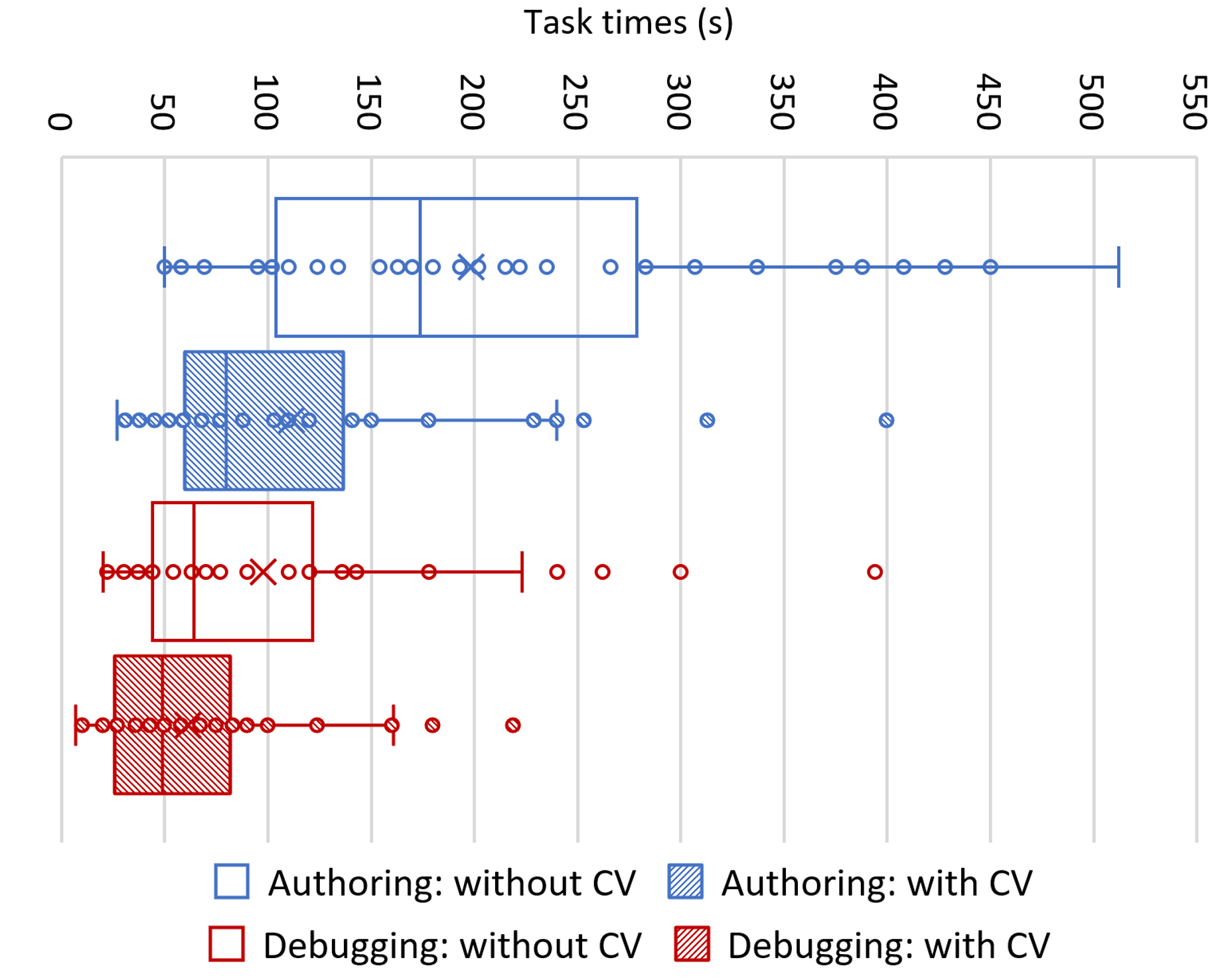
Task times were not normally distributed.⁴ However, they conformed to a lognormal distribution. Due to statistical concerns with the inappropriate application of log normalisation [13] we opted for a nonparametric test.

Cognitive load: Participants reported a lower cognitive load when using CV than without (median difference of -2.25; the TLX is a 21-point scale). This difference is statistically significant (Wilcoxon signed rank test: Z =  − 3.04,p = 0.0024). Cognitive load scores were not normally distributed. See Figure 6.

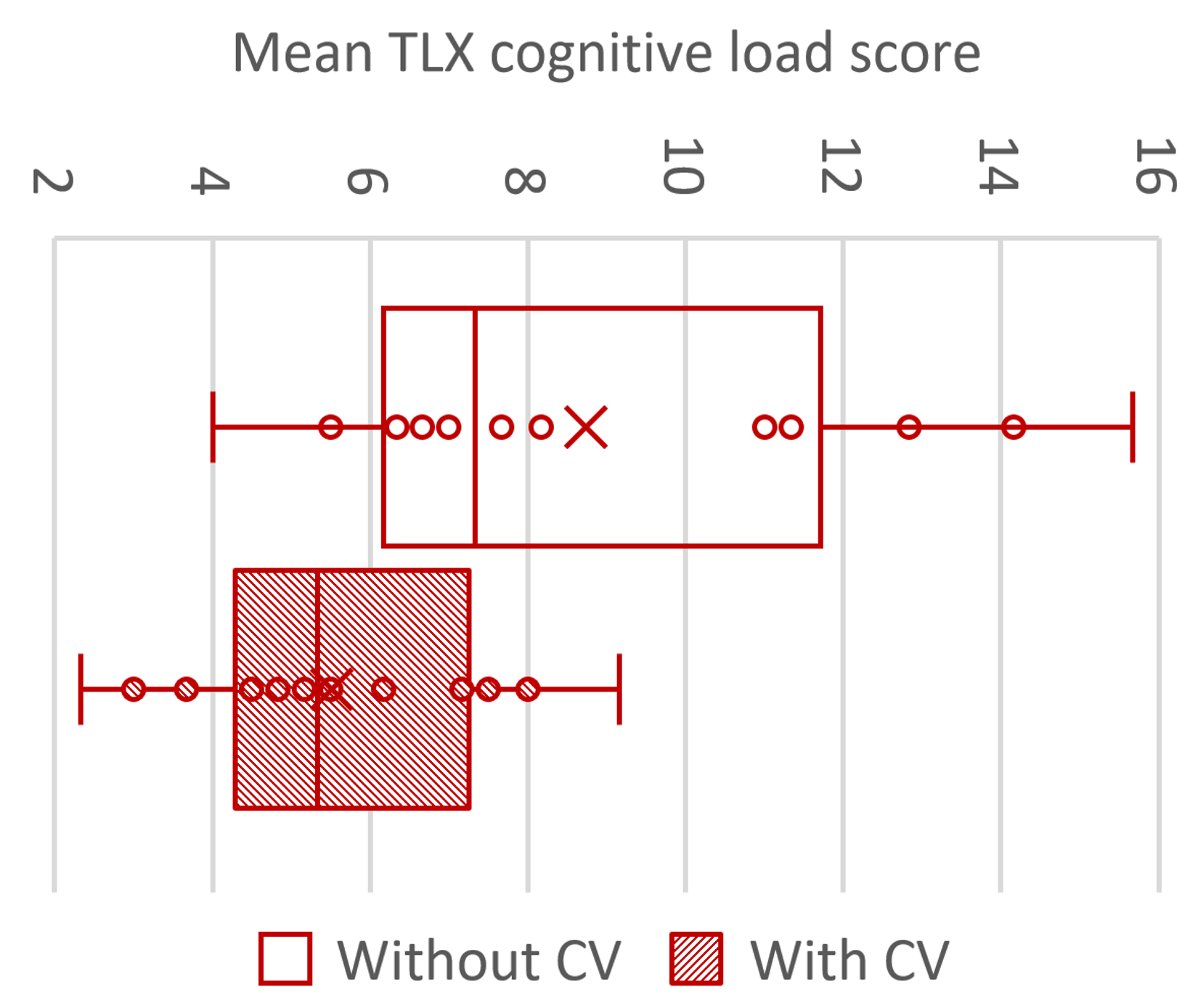
Analysing this result in terms of the six individual items on the TLX questionnaire, it appears as though this difference is attributable to three of them. With CV, there was a lower mental demand (median difference of -2.5), lower effort (median difference of -3), and lower frustration (median difference of -2.5). Of these, only the difference in frustration was statistically significant with Bonferroni correction applied (Wilcoxon signed rank test: Z =  − 3.12,p = 0.0018)

Self-efficacy: Participants had a slightly higher self-efficacy when using CV than without (median difference of 0.28; self-efficacy is a 10-point scale). This difference is not statistically significant. No individual item on the self-efficacy questionnaire showed significant differences between the with and without-CV conditions. We view this as a positive outcome, as it shows that the beneficial effects of shorter task times and lower cognitive load does not come at the cost of a reduced self-efficacy, which is sometimes the case when participants are asked to interact with a system that is more complex than what they are familiar with.

Effect of previous spreadsheet experience: participants were categorised into two groups based on their responses to the spreadsheet expertise self-assessment. Eleven participants fell into a ‘higher’ expertise group (H) and the other 11 into a ‘lower’ expertise group (L). Higher expertise was characterised by a prior knowledge of spreadsheet features relevant to our tasks (formulas, range notation, and drag-filling) as well as practical experience in applying these features. Lower expertise participants lacked knowledge, experience, or both.

While both H and L participants reported lower cognitive load overall, seven H participants reported a lower physical demand with CV, in comparison to only three L participants. Most L participants did not perceive drag-filling as physically demanding, despite the fact that experienced participants typically have developed coping mechanisms to deal with large drag-fill operations (e.g., checking the ranges beforehand, zooming the spreadsheet outwards, making selections using keyboard shortcuts) that reduce the physical effort of drag-filling. This is attributable to the fact that H participants apply drag-fills more regularly and so are more sensitive to the reduction in physical effort afforded by CV.

Revisiting task times, it appears as though H and L participants benefited to a very similar extent for debugging tasks (36.7% median speed-up for group H, 44.28% median speed-up for group L). However, L participants benefited to a greater extent during authoring tasks (55.3% median speed-up for group L, versus only 13.5% median speed-up for group H). Again, this can be attributed to the fact that H participants had developed better coping mechanisms that allowed them to be more efficient at drag-filling operations.

We did not observe a statistically significant difference in self-efficacy scores within either group H or L in isolation.

6 Multiple representations in spreadsheets

Calculation View’s fundamental idea is simple: provide a view of a spreadsheet that is optimised for understanding and manipulating its computational structure. This apparently straightforward idea has revealed a complex design space, the surface of which we have only scratched. In this section we describe alternatives that we have considered, or which might be scope for future work.

Variations of range assignment

What if you want to assign a single formula to a non-rectangular range, or even to disjoint ranges? Since the comma operator already denotes range union in Excel, we could allow it on the left hand side of an assignment, thus:

    B1:B10, C1:C5, D7 = SQRT(A1)

Excel’s drag-fill also allows for constructing sequences of numbers or dates, such as 1,3,5,7... in a range of cells; manually type the first few entries, select them, and drag-fill. In CV, this will appear as a large number of literal assignments, concealing the user intent. We might instead imagine using ellipsis as a notation to indicate sequence assignment:

    B1:B10 = 1,3,5,7...

Similarly, imagine that the cells A1 and B1 contain two distinct formulas. The user may select both and drag-fill downwards to copy. In CV, the user would have to make two edits, since they are two separate range assignments. We might instead provide a notation to capture this, for instance:

    A2:B10 = copy A1:B1

Variations on the editing experience

The current CV editor inhabits a space between textual programming and the grid, in order to improve usability for non-expert end-users. However, for experts (e.g., with programming experience), we could use an existing, generic IDE framework (e.g., Visual Studio Code) as the editor for CV, where the expert programmer could rely on familiar affordances, including syntax highlighting, auto-complete, etc.

Textual notations have the capacity to solve a certain set of problems in spreadsheet interaction, but alternative representations might be better suited for solving different kinds of problems. Some sketches are shown in Figure 7. For instance, the editor could employ a blocks-style visual language, which would prevent syntactic errors. Alternatively, the editor could display formulas within a flow chart diagram, emphasising the dependencies between cells. In fact, the editor could display any number of spreadsheet-based visual programming languages, as long as the correspondence between the two representations was carefully considered. Users could then switch representations according to the task at hand.

Data specific to the alternative representation

Some content is present in the grid view, but not CV (e.g. cell formatting); but not the other way round. That is, the CV can be generated automatically, simply from the existing spreadsheet (Figure 3). However, a more expert programmer might want to do more in calculation view, such as using comments within formulas, and grouping together related assignments, even if they are not adjacent in the grid. In order to enable these types of secondary notation, additional information needs to be persisted within the file that is present in CV but not presented or editable in the grid.

Professionally written code is typically kept in a repository, and subject to code review, version control, and other engineering practices. If we could express all the information about a spreadsheet in textual form, these tools could also be applied to spreadsheets.

7 Related work

7.1 Multiple representations and spreadsheet visualisation

Multiple representations have previously been applied in spreadsheets in the interactive machine learning domain [14], but not as simultaneous editing experiences. Programming languages theory has a concept of ‘lenses’ [15] which is a form of infrastructure enabling multiple representations. One application of lenses to spreadsheets [16] allows the user to edit the value of a formula, and have the edit propagate back to the cell’s input to the formula.

Previously explored approaches to mitigate computation hiding in spreadsheets include identification and visualisation of groups of related cells using colour [17]. Surfacing parts of the dataflow (cell dependency) graph, and allowing the graph to be directly manipulated, has also been explored [18]. Visualising the relationship between different sheets has also been shown to be beneficial [19]. Several commercial tools aim to assist with editing and debugging spreadsheet formulas, often via capabilities for visualisation.⁵

7.2 Overcoming spreadsheet errors

There are broadly two approaches to the mitigation of spreadsheet errors. The first approach is auditing tools, which rely on heuristics such as code smells [20]–[22] or type inference [23], [24], or assist users to write tests [25] to identify and report potential errors. They are not always effective [26], and they are limited by their post-hoc nature (i.e., they help users find errors after they have been made, rather than helping users avoid them in the first place), as well as their heuristics – they cannot detect errors not anticipated by developers of the tool. A machine learning approach where a model is trained on an error corpus [27] is unlikely to mitigate this latter limitation – here the heuristics are exemplified by the training dataset, rather than hand-coded.

The second approach to error mitigation in spreadsheets focuses on altering the structure of the grid, or creating an enhanced formula language. For example, sheet-defined functions [28] allow users to define custom functions in the grid. The Forms/3 system [29] focuses on the design space between grids and textual code. Representations such as hierarchical grids [30] support better object orientation in grids, sometimes combined with a richer formula language [31]. These formula languages can become sophisticated abstract specification languages that support ‘model-driven’ spreadsheet construction [32]–[34]. Excel’s ‘calculated columns’⁶ apply a single formula to an entire column, but using a more abstract ‘structured reference’ syntax, and there is no way to create a calculated ‘row’ or ‘block’. Excel’s array formulas⁷ use an abstract syntax to assign a single formula to a block of cells, but violate Kay’s ‘value principle’ [35] by forbidding inspection or editing of any of the constituent cells except the header. Solutions of this second approach address the poor abstraction gradient in spreadsheets [36], but require substantially greater expertise to use.

8 Conclusions and next steps

Our initial study has demonstrated that a textual calculation view of a spreadsheet, adjacent with the grid view, can make spreadsheets more comprehensible and maintainable. We plan to develop our prototype, exploring a number of variations, including using a free-form text editor, view filtering and navigational support, and enhanced syntax for assignments.

References